ATSC Transmissions with Gnu Radio

Gary Schafer, May 2025

ATSC, for whatever reason, interested me recently. It's not the first time. This time, however, I want to be able to both transmit and receive digital video.

Gnu Radio has the ability to both receive and transmit ATSC signals. (NOTE: As of this writing, most ATSC signals are version 1.0; some stations are starting to switch to version 3.0, which is also called "NextGen TV". This post will only look at version 1.0. It is the only version that Gnu Radio can currently handle.) I tried the receiver on some local signals. I even achieved some success. I really wanted to know how it handled signals in pristine condition. That meant making them myself. The problem is the lack of information on how to make the transmitter work.

Gnu Radio has a page that shows you how to make an ATSC Version 1 signal. Unfortunately, the flowgraph uses a file source that has the filename "advatsc.ts". Where does that file come from?

I figured it out. Making an ATSC signal is a two (or three) step process, depending on what you want to do with the signal.

1. Convert the MP4 video to a MPEG2 transport stream (TS) using ffmpeg.
2. Convert the TS to ATSC Ver 1 using Gnu Radio Companion. At this point, you have a pristine ATSC Ver 1 signal that you can use to test the ATSC receive blocks.
3. Transmit ATSC to television. I've tested this with both a HackRF One and a Ettus Research B200-mini. It worked fine for both.

Tools Needed for Recreating ATSC Video

To recreate a ATSC video signal, aside from the need of a computer (or other processor), I used the following:

• A MP4 video. I'm using a video I took at Cornell University of the Cornell Chimes.
• ffmpeg.
• Gnu Radio Companion.
• VLC
• A transmit-capable SDR with at least 6 MHz of realtime bandwidth. I've tested this on the HackRF One and the Ettus Research B200-mini. It worked fine on both.

Converting MP4 Video to a Transport Stream

ATSC works not on a video signal, but a transport stream based on the MPEG2 standard. That's the ".ts" in the file source from the Gnu Radio Companion wiki page on ATSC. Think of a transport stream as a stream of digital data that consists of video, audio and other data. It most likely is even multiple video, audio and data streams put together into one, huuuuuuge stream. The first step is to take a video file and convert it to the appropriate transport stream.

I opened a terminal and navigated to the folder containing my MP4 file. I used the following "ffmpeg" command to create the transport stream file:

ffmpeg -i cornell-chimes.mp4 -c:v mpeg2video -b:v 3000k -acodec ac3 -b:a 768k -ar 48k -ac 2 -muxrate 19392658 -f mpegts cornell-chimes.ts

where:

• -i cornell-chimes.mp4: This is my input video file that will be translated into the MP2 transport stream.
• -c:v mpeg2video: This explicitly tells the ffmpeg command to convert the output video to the MPEG-2 standard.
• -b:v 3000k: This says to convert the file to a bitstream with an output bitrate of 3 Mbps (3000 x k = 3000 x 1000). This bitrate directly affects the quality of the resulting video signal.
• -acodec ac3: This says to make the output audio into the AAC3 standard (I think). NOTE: I've seen some commands in which this is "eac3", which is "enhanced AAC3". I've had less luck with that audio standard.
• -b:a 768k: This says to make the audio output bitrate at 768k. This is 48 kHz at 8 bits/sample times two channels (stereo, left and right).
• -ar 48k: This says to make the audio sample rate 48 kHz.
• -ac 2: This says that there are two audio streams (stereo, left and right).
• -muxrate 19392658: This is the raw bit rate for data on a ATSC version 1.0 signal. The calculation is 2.25e6/143*684*3*312/313*2/3*188/208 = 19392658.
• -f mpegts: This says to make the output a MPEG transport stream.
• cornell-chimes.ts: This will be the output transport stream file that you can then plug into the "File Source" in the GRC flowgraph.

Converting TS File to an ATSC Signal

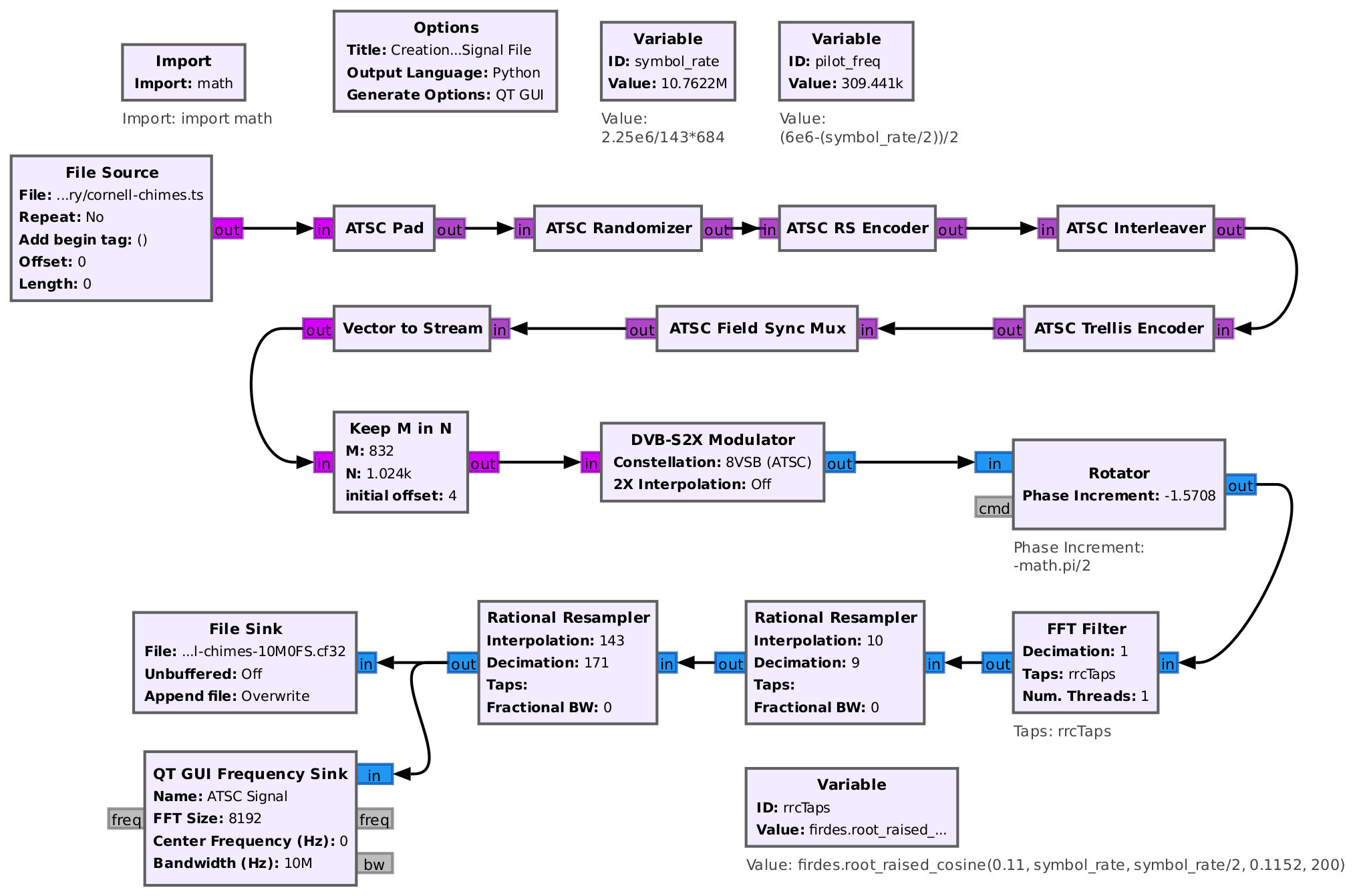
I used the following Gnu Radio Companion flowgraph to convert the TS file to an ATSC signal. NOTE: The flowgraph is using two "Rational Resampler" blocks because I'm trying to get a final sample rate of 10 MHz. Given that, it's possible to both create the ATSC signal and transmit it at the same time, but in my experience, this requires a beefy computer. Even then, there's no guarantee that you will not experience a fair number of underflows. Let me explain it another way. I'm using an Intel, 13th generation, i9 processor, and I still got a fair number of underflows when running the flowgraph while transmitting at the end rather than saving to a file.

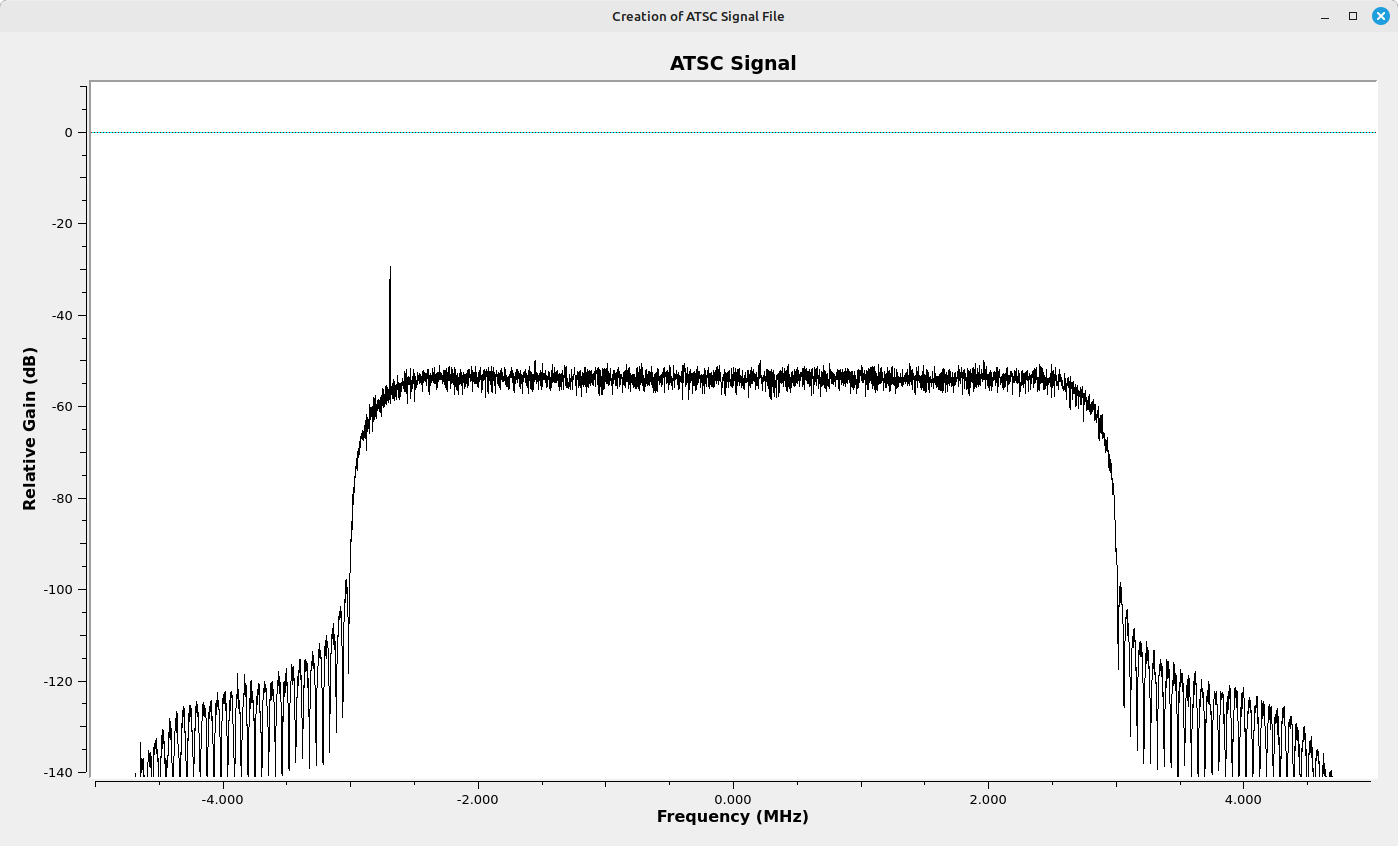
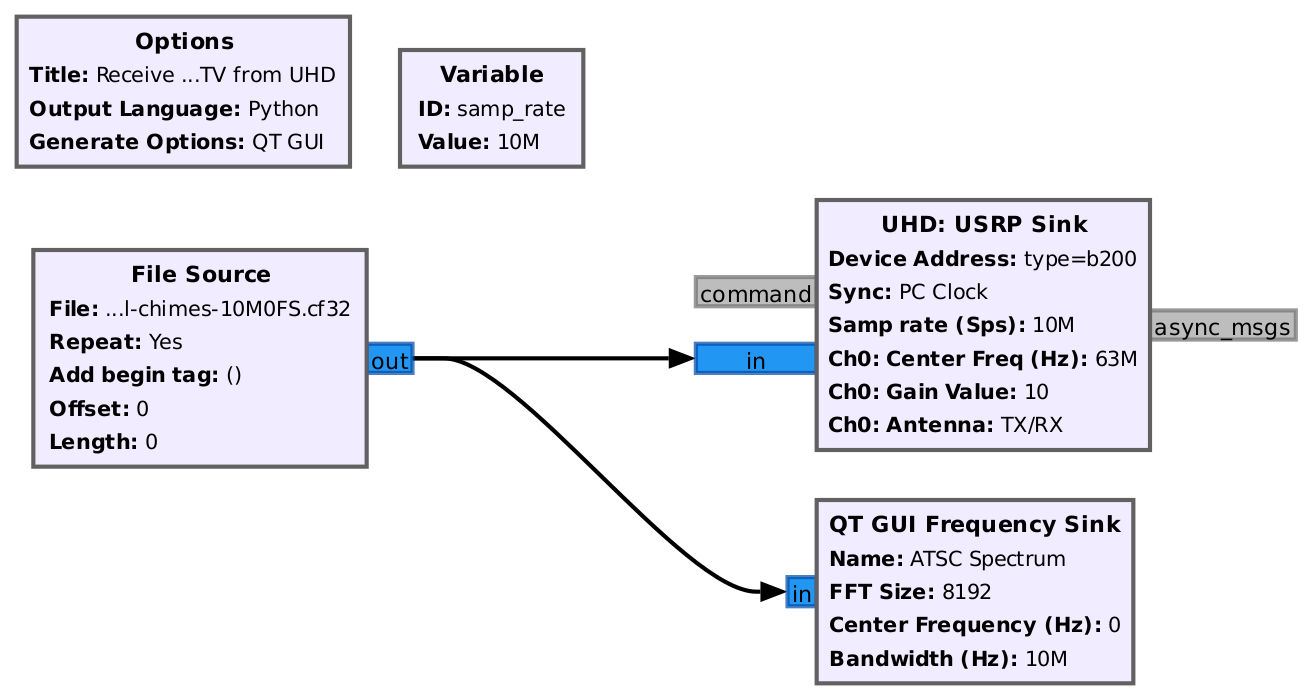
Using Gnu Radio to Receive the Stored ATSC Signal

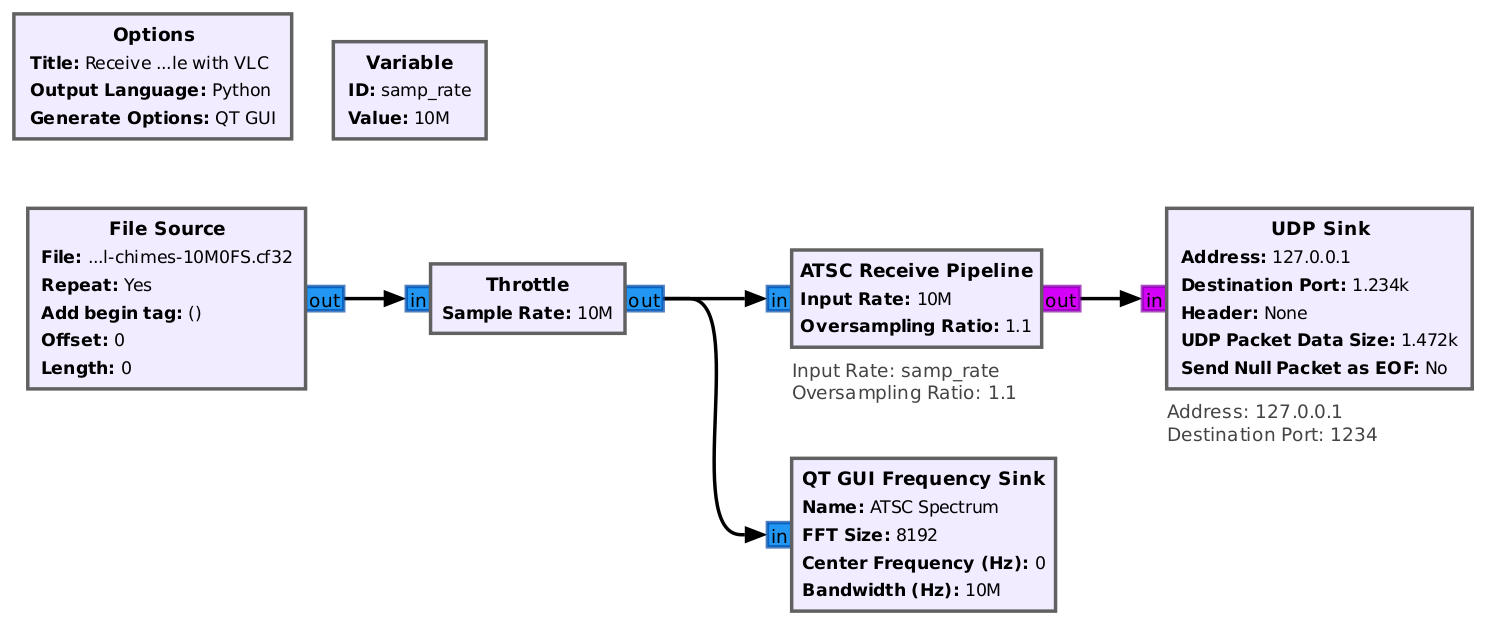
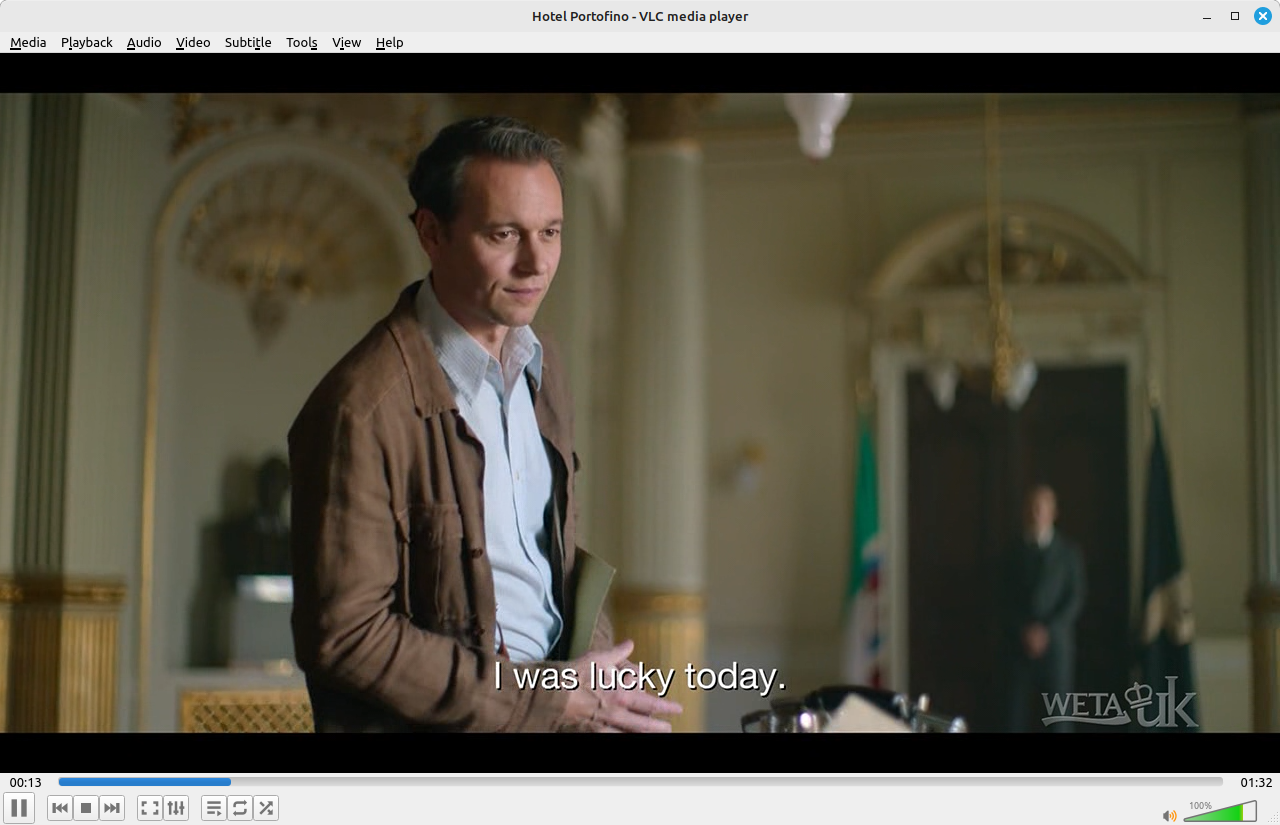
This gave me my "perfect" ATSC signal, which I can then use to test the ATSC receive block in Gnu Radio. I created a basic flowgraph sending the ATSC samples directly into the "ATSC Receive Pipeline" block. The output is the transport stream. I used a UDP sink block to stream the transport stream to VLC.

Once the flowgraph was running, I opened VLC, set the network stream parameters, and hit "Play". The result is shown below.

Using Gnu Radio to Transmit a Live ATSC Signal

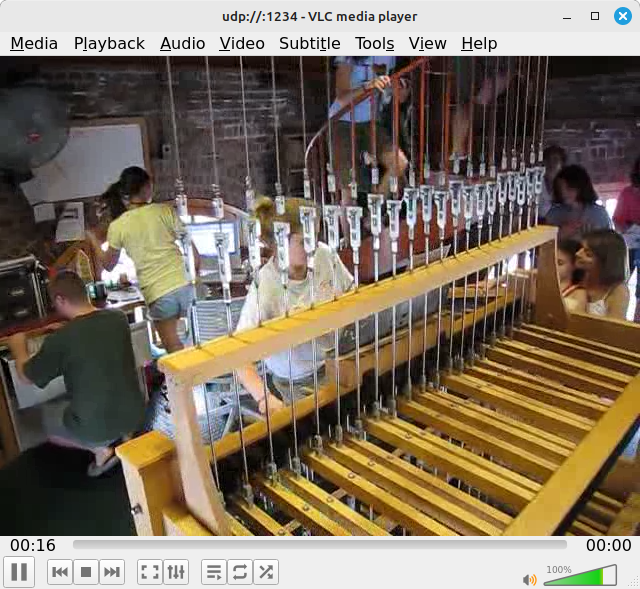
For my second test, I transmitted the ATSC signal from my Ettus Research B200-mini to a television. NOTE: I used a cable to direct connect so as not to run afoul of any FCC regulations. The results were just as you would expect.

I set the center frequency of the B200-mini to 63 MHz, which in the USA is the center frequency for channel 3. The television I used (an older Toshiba) allows for direct tuning to an ATSC signal for channel 3 by entering "3-1" using the remote control.

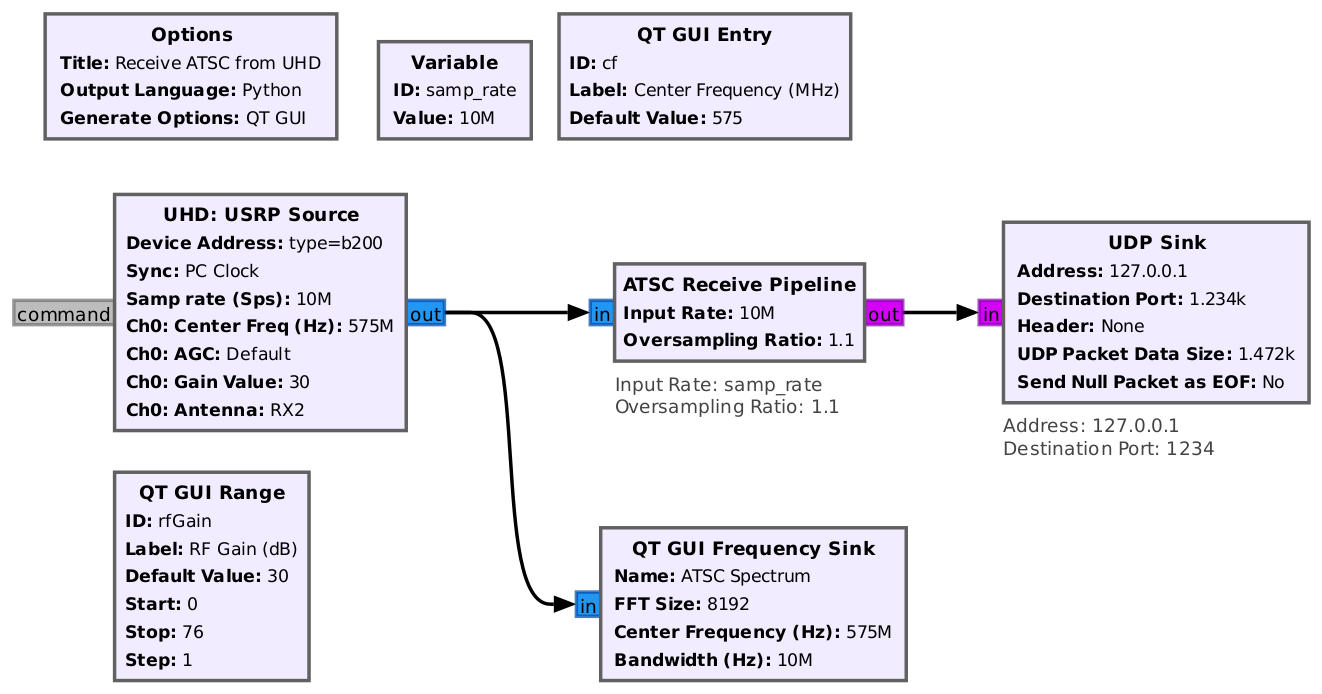
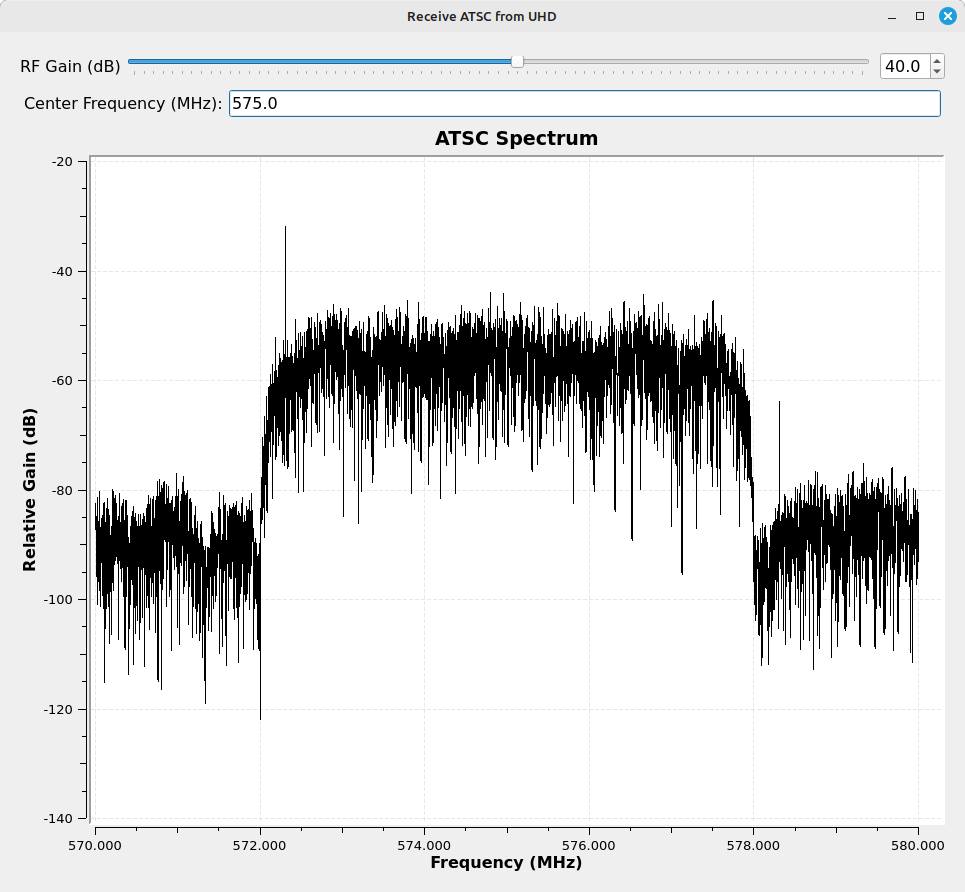
Using Gnu Radio to Receive a Live ATSC Signal

Once I had a better idea of recovering ATSC signals, I went back and re-looked at recovering, live, over-the-air ATSC signals. It turns out that the Gnu Radio receive block needs two things to recover live ATSC signals. These are:

1. A strong ATSC signal. Anything close to the noise floor will most likely be unrecoverable.
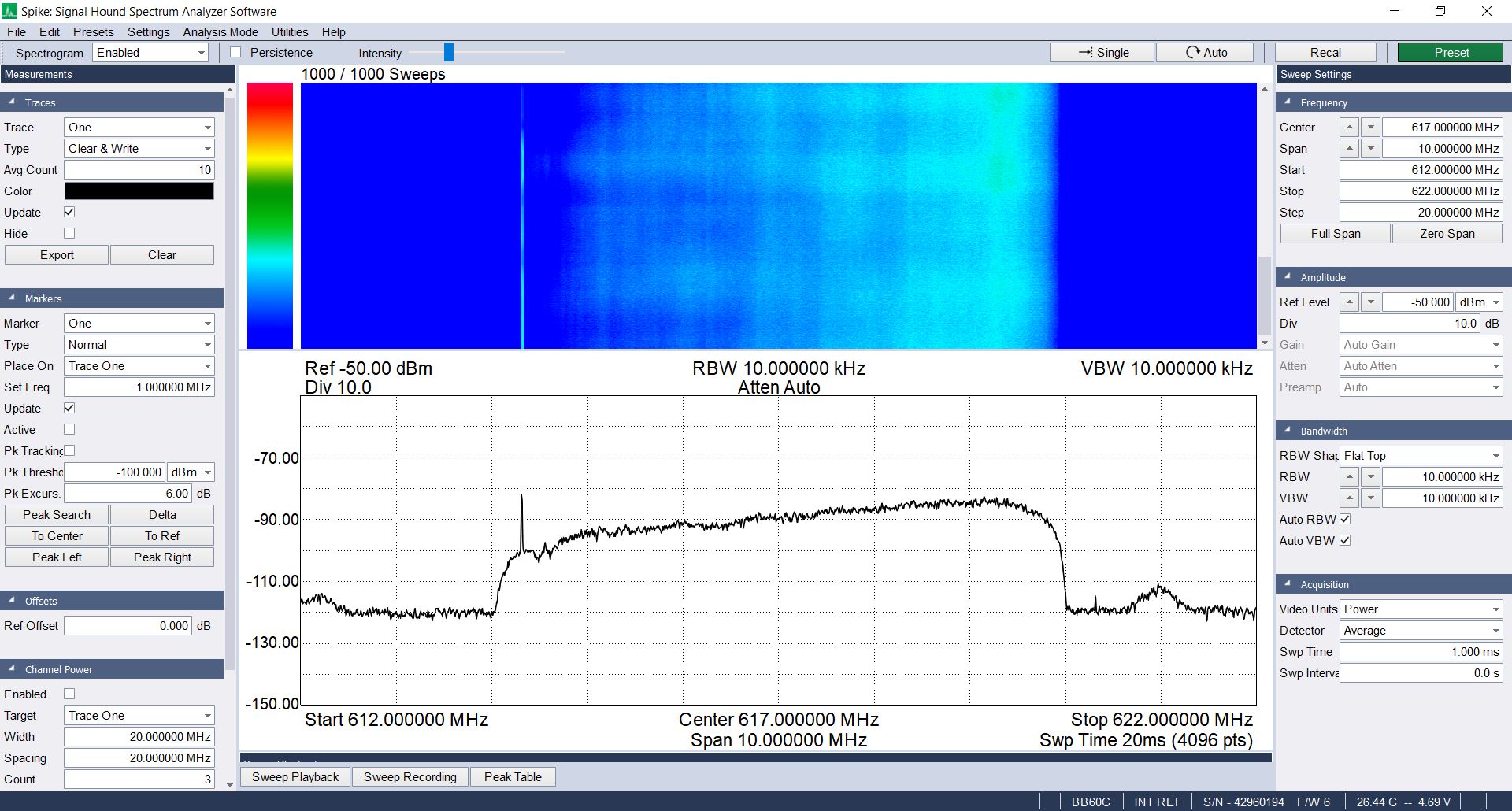
2. A flat spectrum. A major problem with ATSC is the fact that it, like many wideband signals, suffers from frequency-selective fading. As I was watching an OTA station (WETA near Washington, DC), I saw the video signal have the occasional drop-out. It correlated with the wind outside. As the wind picked up, the station would drop-out. The signal would recover when the wind faded.

It also turns out that the Gnu Radio flowgraph to recover ATSC is much simpler than I first thought. When I typically tune signals using Gnu Radio, I'll add a filter to get rid of everything except for the signal I want. No need to do that with ATSC. The "ATSC Receive Pipeline" block has the filtering needed.

Summary

ATSC version 1 does provide some advantages over the older (now mostly-defunct) analog video transmissions. The images can have better resolution and fidelity, and each carrier can carry multiple video feeds simultaneously. Recording the direct feed, however, can require a lot of storage. As I stated previously, the ATSC signal consists of a net data stream of roughly 19.393 Mbits/sec. That's 2.424 MB/sec. A 30 minute recording would provide a 4.36 GB file.

I hope this helps you to look more into Gnu Radio and ATSC signals. Til next time!